1. Introdução
A definição de força da gravidade, adotada em textos clássicos de Geodésia (Vanicek & Krakiwski, 1986; Gemael, 1981; Zakatov, 1962), é dada como a soma da força gravitacional com a força centrífuga. Essa definição pode surpreender alguns iniciantes em Geodésia, acostumados com textos da Mecânica Clássica que evitam ou consideram injustificado o uso de uma força centrífuga em estudos da Dinâmica dos corpos em rotação (Sears et al., 1985, p.109; Meriam, 1976, p.181).
De acordo com Symon (1982) “Existe uma grande confusão em relação ao termo força centrífuga, que, na realidade, não é uma força, pelo menos na Mecânica Clássica, e não estará presente se se faz referência a um sistema de coordenadas fixo no espaço ”.
A definição do sistema de referência é o real motivo dessa confusão aparente, nos estudos de corpos em rotação. O tipo de sistema de referência adotado nem sempre está claro nos textos que tratam do assunto. O uso frequente de um sistema de coordenadas não inercial, nesses estudos, torna conveniente o uso do conceito de força centrífuga, considerada como um tipo de força inercial ou pseudoforça (Resnick et al., 1992). Por outro lado, quando se adota um referencial inercial, o conceito de força centrifuga não faz sentido e o mesmo ocorre com a força da gravidade, que é definida a partir dessa. Se a aceleração de um corpo é medida com base em um referencial acelerado, em relação a um referencial inercial, a força resultante sobre esse corpo não é igual à sua massa vezes a sua aceleração. Para tornar a Lei de Newton válida, nesses casos, pode-se introduzir as chamadas forças inerciais, que dependem da aceleração do referencial (Tipler, 1985). Simula-se, assim, um estado de equilíbrio e pode-se estudar o problema pelos métodos da Estática. Dessa forma, um corpo submetido a uma força centrípeta é equilibrado por uma força centrífuga, de mesma intensidade, mas de sentido oposto. Beer e Jonhston (1991) mostram alguns exemplos de como forças inerciais, simulando equilíbrio dinâmico do sistema de forças, podem ser usadas para simplificar a solução de problemas.
BONFORD (1980), em sua definição de gravidade: “the vector sum of the acceleration due to the attraction of the earth, and that due to the centrifugal force arising from the use of rotating axes of coordinates”, deixa claro que a força centrífuga surge devido ao sistema de referência empregado (maiores detalhes nos §5.00, §6.08 e Appendix I, dessa referência).
Neste Texto faz-se um resumo bibliográfico sobre o conceito e aplicação de força centrífuga e de seu uso na definição de força da gravidade. Analisa-se, também, o caso da composição de forças que agem em um corpo situado na superfície física da Terra, considerando-se um referencial inercial.
2. Forças Inerciais
O conceito de força inercial surge da adoção de um sistema de coordenadas não-inercial na explicação de fenômenos físicos em Dinâmica. Meriam (1976, p.180 e 254) explica esse problema tomando-se eixos de referência fixos a um corpo rígido que executa um movimento plano geral. Um observador, fixo a esses eixos, não pode medir qualquer movimento do corpo em relação ao seu sistema de referência móvel. O observador supõe, assim, que o corpo está “equilíbrio”. A única forma de traduzir esse estado artificial de equilíbrio, de modo coerente, é pela imposição de uma força fictícia de mesma intensidade e sentido contrário à força resultante que atua sobre o corpo, segundo um sistema de referência inercial. Essa força fictícia é chamada de força inercial. Meriam (1976, p.180), que é contra o uso desse método, lembra que a transformação aparente de um problema de Dinâmica em um de Estática tornou-se conhecido como Princípio de D’Alembert, devido ao Traité de Dynamique de D’Alembert, publicado em 1743, que abordava problemas sob esse ponto de vista.
O conceito de força centrífuga, caso especial de força inercial, pode ser entendido com o auxílio do vagão de trem esquemático da Fig.1, que descreve uma curva para a esquerda, em movimento circular uniforme. Uma esfera de massa m está presa ao teto do vagão por uma corda. Um observador, em terra, considera que a deflexão observada na corda, deve-se simplesmente à tendência da esfera de manter seu estado de inércia. No entanto, um observador no interior do vagão vê a esfera como se uma força f, atuando sobre ela, fosse a responsável pela deflexão da corda. Essa força inercial f, atuando “para fora” e perpendicular à tangente à curva descrita pela esfera, é tradicionalmente denominada de força centrífuga.
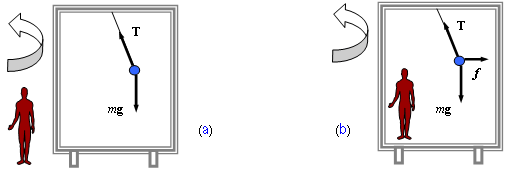
Fig. 1 - Exemplo esquemático de um vagão de trem fazendo uma curva para a esquerda. Uma esfera de massa m e sujeita à aceleração da gravidade g, está presa ao teto do vagão por uma corda, com uma tração T. No exemplo (a), um observador inercial, em relação ao solo, vê a esfera fazer a curva, junto com o vagão, com uma aceleração centrípeta dada pela componente horizontal de T. Para um observador dentro do vagão, que sofre a mesma aceleração deste, a esfera está em equilíbrio e, por isso, é necessário uma força fictícia f que equilibre a componente horizontal de T. [Adaptação de TIPLER (1985, p.142)].
Alonso & Finn (1972) desenvolvem o seguinte raciocínio para justificar analiticamente uma força inercial:
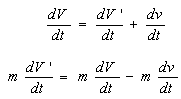 |
(1)
(2) |
Os termos de (2) têm a dimensão de força, sendo que a força que atua em m, medida pelo observador inercial, é F = m dV/dt. De acordo com Alonso & Finn, se o observador não-inercial adotar a mesma definição de força ele medirá uma força F’ = m dV/dt. Tem-se, dessa forma, que:
![]() (3)
(3)
Alonso & Finn denominam o termo – m dv/dt de “uma força fictícia chamada força inercial”. Note que, se os dois observadores O e O’ fossem inerciais, ou seja, possuíssem velocidades relativas constantes em relação a um sistema inercial, v seria constante e, consequentemente dv/dt = 0. Nesse caso, a consideração de uma força inercial (ou de uma força centrífuga no caso de movimentos de rotação), para descrever o movimento da partícula, não faria nenhum sentido.
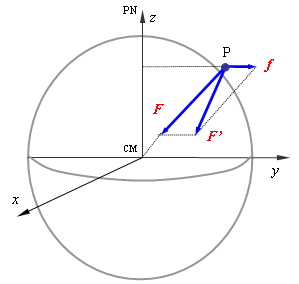
Fig. 2 - Representação da composição vetorial da força da gravidade F’ como a soma da força de atração gravitacional F com a força centrífuga f. As forças atuam sobre uma partícula situada em um ponto P referido a um sistema de coordenadas não-inercial, geocêntrico e que gira solidário à Terra.
3. Força da Gravidade em Referenciais Não-Inerciais
No estudo do movimentos de corpos próximos à superfície da Terra é conveniente o uso de sistemas de coordenadas que giram solidários à Terra. Esses sistemas são do tipo não-inercial e induzem à consideração de forças inerciais quando se deseja explicar os movimentos dos corpos sobre a superfície da Terra.
Bonford (1980, p.398) explica que a rotação da Terra pode ser ignorada e um ponto P qualquer, fixo à Terra, pode ser considerado estacionário quando adotamos uma força centrífuga w2p, atuando em cada partícula de massa unitária, onde w é a velocidade angular e p é a perpendicular tomada de P ao eixo de rotação. Essa perpendicular dá a direção da força centrífuga que atua no sentido “para fora” do movimento de rotação da Terra.
A Fig.2 representa esquematicamente a força da gravidade, F’, como a composição vetorial da força centrífuga, f, e da força gravitacional, F, atuando sobre uma partícula em P, com base em um referencial (x, y, z) não-inercial que gira solidário à Terra.
4. Composição de Forças em Referenciais Inerciais
O conceito de força centrífuga não é amparado pela Mecânica Clássica, pois ela só existe se adotamos um referencial não-inercial. A força da gravidade, sendo deduzida a partir da força centrífuga, também só aparece quando usamos um referencial não-inercial.
A Fig.3 mostra um paralelepípedo situado sobre a superfície física da Terra e sujeito à ação da gravidade. A composição de forças que atuam sobre o paralelepípedo, como indicada na Fig.3, é uma adaptação das abordagens apresentadas por Sears et al. (1985, p.117) e Resnick et al. (1992, p.349). Desprezando-se o movimento orbital da Terra, pode-se considerar o sistema de coordenadas geocêntrico (x’, y’, z’) como um referencial inercial (não girante com a Terra). Supondo-se a Terra esfericamente simétrica e com rotação constante, o paralelepípedo está em movimento circular uniforme, com raio dado pela sua distância ao eixo de rotação, tomada perpendicularmente a este. De acordo com as duas primeiras Leis de Newton da Mecânica Clássica, existe uma força resultante atuando sobre o paralelepípedo, que é a força centrípeta fc, perpendicular ao eixo de rotação e responsável pelo seu movimento circular. Essa força centrípeta é a resultante da força gravitacional, F, que age sobre o paralelepípedo, e da força N provocada pela superfície da Terra que impede o seu movimento, em direção ao centro da Terra, devido à atração gravitacional (usualmente chamada de força normal).
A força centrípeta fc tem a mesma direção e intensidade da força centrífuga w²p, do Item anterior, mas sentido oposto. Percebe-se intuitivamente que tanto N quanto fc são “sustentadas” pela própria força gravitacional. Isso pode ser melhor percebido colocando-se o paralelepípedo da Fig.3 no equador. Nessa posição, as três forças que atuam sobre o paralelepípedo alinham-se sobre o eixo y’. Se imaginamos a rotação da Terra aumentando até que w²p > F, o paralelepípedo irá seguir na direção da tangente ao seu movimento, entrando em órbita da Terra com a sua velocidade tangencial nesse momento. No caso inverso, se imaginamos w = 0, o paralelepípedo estará em equilíbrio estático e F e N terão mesma intensidade e direção, mas sentidos opostos.
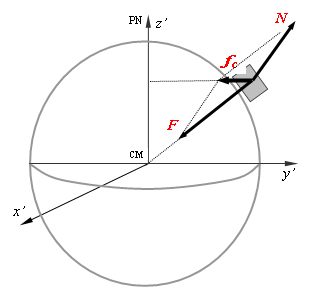
Fig. 3 - Composição de forças atuando sobre um paralelepípedo situado sobre a superfície da Terra, considerando-se um ref. inercial. F é a força gravitacional, N é uma força normal e fc é a força centrípeta.
5. Considerações Finais
Sob os olhos da Mecânica Clássica, que se fundamenta em referenciais inerciais, a força da gravidade não se traduz como uma grandeza física, uma vez que uma de suas componentes, a força centrífuga, somente é adotada em referenciais não-inerciais. Essa idéia é reforçada pelo fato de que a força centrífuga contraria a 3a Lei de Newton, pois não existe uma força de reação a ela.
Em Geodésia Espacial, o estudo do movimento dos satélites não considera normalmente a força centrífuga, pois é mais útil se usar referenciais não girantes com a Terra. Como a força centrífuga é proporcional à distância ao eixo de rotação, ela tem uma intensidade algumas vezes maior para as órbitas dos satélites mais afastados. Bonford (1980, p.424), em sua abordagem da gravidade em altitudes de órbitas de satélites, fornece uma equação para calcular o potencial gravitacional, utilizando eixos girantes com a Terra e o conceito de força centrífuga (através do potencial centrífugo). Bonford, entretanto, faz a seguinte observação quanto ao uso desse método para o estudo do movimento de satélites: “This is unlikely to be required”.
Do ponto de vista geodésico, é muito útil o uso de referenciais não-inerciais, com as forças inerciais decorrentes dessa opção. O estudo da gravidade, com base em referenciais inerciais, pode se tornar muito complexo. Para Marion (1965) a utilidade do conceito de força centrífuga é obvia, pois a descrição do movimento de uma partícula com relação a um corpo que gira relativamente a um referencial inercial é claramente um problema complicado.
*Sobre o autor: Jonildo Bacelar é engenheiro eletricista, geodesista e editor do Guia Geográfico.
Referências Bibliográficas
Alonso, M.; Finn, E.J.; Física – Um Curso Universitário, vol. I – Mecânica; Editora Edgard Blucher, São Paulo, 1972.
Beer, F.P.; Jonhston Jr., E.R.; Mecânica Vetorial para Engenheiros – Cinemática e Dinâmica. 5a. edição, Makron Books; São Paulo, 1991.
Bonford, G.; Geodesy., Clarendon Press, Oxford. 855p., 4ª edição em 1980, reimpressão com correções em 1983.
Gemael, C.; Introdução à Geodésia Física. CPGCG / UFPR, Curitiba, 1981.
Marion, J.B.; Classical Dynamics of Particles and Systems. Academic Press, London, N.York, 1965.
Meriam, J.C.; Dinâmica (tradução do original Dinamics, 1966); Livros Técnicos e Científicos Editora. Rio de Janeiro, 1976.
Resnick, R.; Halliday, D.; Krane, K.S; Physics vol.1; 4th edition. John Wiley & Sons, INC. N. York, 1992.
Sears, F.; Zemansky, M.W.; Young, H.D.; Física 1 – Mecânica da Partícula e dos Corpos Rígidos, 2a. edição; Livros Técnicos e Científicos Editora; Rio de Janeiro, S. Paulo, 1985.
Symon, K.R.; Mecânica. Editora Campos. Rio de Janeiro, 1982).
Tipler, P.A.; Física, vol. 1a. 2a. edição. Guanabara Dois, Rio de Janeiro, 1985.
Vanicek, P. & Krakiwski, E. J.; Geodesy: The Concepts. North Holland Publishing Company; 2a. edição; Netherlands, 1986.
Zakatov, P.S.; A Course in Higher Geodesy. Tradução do original em russo. National Science Foundation, Washington D.C., 1962.
